Zusammenfassung

• Eine gedämpfte Schwingung kann durch die Funktion

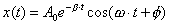  beschrieben werden.

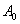• ist die Amplitude der Schwingung ohne Dämpfung.
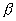• ist die Abklingungskonstante.
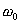• ist die Eigenfrequenz des Oszillators ohne Dämpfung
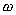• ist die Kreisfrequenz der Schwingung und es gilt:

• Für 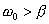tritt der Schwingfall ein.
• Für 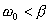tritt der Kriechfall ein, bei dem der Oszillator die Ruhelage nicht mehr passiert.
• Für 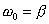tritt der aperiodische Grenzfall ein, bei dem die Ruhelage am schnellsten erreicht wird.
• Das Argument der Funktion nennt man die Phase.
• Für den Fall, dass die Schwingung nicht mit der maximalen Auslenkung beginnt wird das Argument um eine sogenannte Phasenkonstante 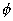erweitert. Sie gibt den Wert der Phase zum Zeitpunkt t =0 an.