Das gedämpfte Federpendel
Wie wir gesehen haben, hängt bei der gedämpften Schwingung:
- Die Frequenz von der Größe der Eigenfrequenz
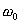 und der Abklingungskonstanten
und der Abklingungskonstanten 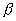 ab.
ab.
- Die Eigenfrequenz wiederum hängt von der Masse m
des Systems und der
Federkonstanten D ab.
- Die Abklingungskonstante von der Masse m und der Reibungskonstanten
r ab.
Oder:
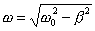 ,
,
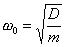 und
und
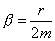 .
.
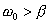 ,
also
,
also
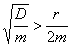 führt
zum Schwingfall.
führt
zum Schwingfall.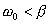 ,
also
,
also 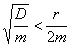 führt zum Kriechfall.
führt zum Kriechfall.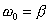 ,
also
,
also 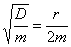 führt zum aperiodischen Grenzfall.
führt zum aperiodischen Grenzfall.
Um
ein Gefühl für diese Zusammenhänge zu entwickeln, steht Ihnen hier
eine Simulation zur Verfügung.
- In dieser Simulation entspricht b der Reibungskonstanten
und k der Federkonstanten.
- Eine Federkonstante von k=16 N/m und eine Masse
von m=1 kg ist voreingestellt.
- Drücken Sie zunächst den Resetbutton in der Simulation.
- Lenken Sie die Feder auf +5 cm aus und drücken Sie den Startbutton.
Bei einer Reibungskonstanten von b=0 kg/s können sie
eine harmonische Schwingung beobachten.
- Erhöhen Sie schrittweise die Reibungskonstante, ohne die Simulation
zu stoppen und beobachten Sie wie sich der Schwingungsverlauf ändert.
- Überlegen Sie anhand der obigen Beziehungen, bei welchem Wert der Reibungskonstanten
der aperiodische Grenzfall eintritt.
- Sie können sich diesem Fall in der Simulation auch annähern, denn
der aperiodische Grenzfall tritt ein, sobald die Feder die Ruhelage nicht
mehr passiert. Probieren Sie es einfach mal!!
- Variieren Sie nacheinander die Werte für die Federkonstante
und die Masse und wiederholen Sie das Experiment.
![]() ,
,
![]() und
und
![]() .
.