 |
Thermische Ausdehnung von Festkörpern
Bei Erwärmung dehnt sich ein Festkörper, von ganz wenigen Ausnahmen
abgesehen, aus. Betrachten wir zunächst den Spezialfall eines stabförmigen
Körpers, so wie er in dem hier
gezeigten Experiment verwendet wird.
Der Stab hat anfangs bei der Temperatur t0
die Länge l0 . Wird er nun auf die
Temperatur t erwärmt, so ändert sich seine
Länge proportional zu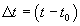 
und proportional zu l0:
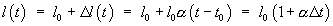
Der Längenausdehnungskoeffizient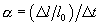 
gilt die relative Längenänderung pro Temperaturintervall an. Er ist
materialspezifisch und selbst leicht temperaturabhängig [Tabelle].
Für nicht zu große Temperaturintervalle (etwa 100 K) kann 
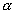in guter Näherung als konstant angesehen werden und liegt typischerweise
in der Größenordnung von 1·10-6 K-1.
Technisch wird die thermische Längenausdehnung beispielsweise für
Bimetall-Streifen genutzt.
Für die Änderung des Volumens V(t)
erhält man analog:
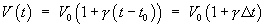
Wobei V0 das Volumen bei
der Temperatur t0 bezeichnet. Für
den Volumenausdehnungskoeffizienten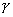 
gilt näherungsweise:
|
|
Der Volumenausdehnungskoeffizient
Das Volumen V(t) eines quaderförmigen Körpers
mit den Kantenlängen a, b und c lässt sich schreiben als
.
Die Kantenlängen sind hier Funktionen der Temperatur t,
wie z. B.
.
Analoges gilt für b und c.
Durch Einsetzen folgt für V(t):
 .
Ausmultiplizieren liefert dann
Da 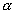sehr
klein ist, können die quadratischen und kubischen Glieder vernachlässigt
werden. Es gilt deshalb
|
|
Thermische Eigenschaften der Materie 
Festkörper und Flüssigkeiten
