Ableitung der Höhenabhängigkeit des Luftdrucks

Betrachten wir eine bestimmte Menge Luft mit der Masse m, die auf der Erdoberfläche, d. h. bei der Höhe h = 0, das Volumen V₀ einnimmt. Ihre Dichte ist folglich

Bei einer beliebigen Höhe h > 0 ändert sich der Druck und damit das Volumen unserer Gasmasse. Die Dichte ist dort

Nach den Boyle-Mariotteschen Gesetz ist aber

Hier bezeichnet p₀ den Druck bei h = 0 und p_h den bei h. Mit Hilfe der Dichten und können wir auch schreiben:

Betrachten wir die Lufthülle als eine Schichtung sehr dünner homogener Luftschichten. Über eine solche Luftschicht der Dicke dh fällt der Druck um

ab. Hier bezeichnet g die Erdbeschleunigung (= 9,81 m s^-2) . Das Minuszeichen deutet an, dass der Druck mit der Höhe abnimmt. Setzen wir hier die obige Beziehung ein, so ist

bzw.

Integration der Gleichung und Beachtung von p_h=0 = p₀ liefert:

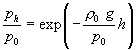
Der Druck nimmt also exponentiell mit der Höhe ab. Setzen wir in diese Beziehung die typischen Werte p₀ = 1013 hPa und = 1,293 kg m^-3 ein, so erhalten wir

Zurück